Incremental and Cumulative Triangle Objects¶

Note

Refer to the Quickstart Guide for invocation examples.

Triangle Functions¶

Within trikit, datasets are transformed into triangle objects by calling totri.

totri(data, tri_type='cum', data_format='incr', data_shape='tabular', origin='origin', dev='dev', value='value')[source]¶

Create a triangle object based on data. tri_type can be one of “incr” or “cum”, determining whether the resulting triangle represents incremental or cumulative losses/counts. If data_shape="triangle", data is assumed to be structured as a runoff triangle, indexed by origin with columns representing development periods. If data_shape="tabular", data is assumed to be tabular with at minimum columns origin, dev and value, which represent origin year, development period and metric of interest respectively. data_format specifies whether the metric of interest are cumulative or incremental in nature. Default value is “incr”.

Parameters

data (pd.DataFrame) – The dataset to be coerced into a triangle instance. data can be tabular loss data, or a dataset (pandas DataFrame) formatted as a triangle, but not typed as such. In the latter case, data_shape should be set to “triangle”.
tri_type ({"cum", "incr"}) – Either “cum” or “incr”. Specifies how the measure of interest (losses, counts, alae, etc.) should be represented in the returned triangle instance.
data_format ({"cum", "incr"}) – Specifies the representation of the metric of interest in data. Default value is “incr”.
data_shape ({"tabular", "triangle"}) – Indicates whether data is formatted as a triangle instead of tabular loss data. In some workflows, triangles may have already been created and are available. In such cases, the triangle-formatted data is read into a DataFrame, then coerced into the desired triangle representation. Default value is “tabular”.
origin (str) – The field in data representing origin year. When data_shape="triangle", origin is ignored. Default value is “origin”.
dev (str) – The field in data representing development period. When data_shape="triangle", dev is ignored. Default value is “dev”.
value (str) – The field in data representing the metric of interest (losses, counts, etc.). When data_shape="triangle", value is ignored. Default value is “value”.

Returns

Return type

{trikit.triangle.IncrTriangle, trikit.triangle.CumTriangle}

Examples

Create incremental triangle based on RAA dataset:

In [1]: from trikit import load, totri
In [2]: df = load("raa")
In [3]: tri = totri(df, tri_type="incr")

Triangle Class Definitions¶

class _BaseTriangle(data, origin=None, dev=None, value=None)[source]¶

Transforms data into a triangle instance.

Parameters

data (pd.DataFrame) – The dataset to be transformed into a _BaseTriangle instance. data must be tabular loss data with at minimum columns representing the origin/acident year, the development period and the actual loss amount, given by origin, dev and value arguments.
origin (str) – The fieldname in data representing origin period.
dev (str) – The fieldname in data representing development period.
value (str) – The fieldname in data representing loss amounts.

static _neg_handler(data, dev, value)[source]¶: Convert any first development period negative values to 1.0.

static _validate(data, origin=None, dev=None, value=None)[source]¶

Ensure data has requisite columns.

Parameters

data (pd.DataFrame) – Initial dataset to be coerced to triangle.
origin (str) – The fieldname in data representing origin period.
dev (str) – The fieldname in data representing development period.
value (str) – The fieldname in data representing loss amounts.

property clvi¶

Determine the last valid index by development period.

Returns
Return type: pd.DataFrame

property devp¶

Return triangle’s development periods.

Returns
Return type: pd.Series

diagonal(offset=0)[source]¶

Return triangle values at given offset. When offset=0, returns latest diagonal.

Parameters: offset (int) – Negative integer value (or 0) representing the diagonal to return. To return the second diagonal, set offset=-1. If abs(offset) exceeds (number of development periods - 1), ValueError is raised. Default value is 0 (represents latest diagonal).
Returns
Return type: pd.Series

property latest¶

Return the values on the triangle’s latest diagonal. Loss amounts are given, along with the associated origin year and development period. The latest loss amount by origin year alone can be obtained by calling self.latest_by_origin, or by development period by calling by self.latest_by_devp.

Returns
Return type: pd.DataFrame

property latest_by_devp¶

Return the latest loss amounts by development period.

Returns
Return type: pd.Series

property latest_by_origin¶

Return the latest loss amounts by origin year.

Returns
Return type: pd.Series

property maturity¶

Return the maturity for each origin period.

Returns
Return type: ps.Series

property nbr_cells¶

Return the number of non-NaN cells.

Returns
Return type: int

property origins¶

Return triangle’s origin periods.

Returns
Return type: pd.Series

property rlvi¶

Determine the last valid index by origin.

Returns
Return type: pd.DataFrame

to_tbl(dropna=True)[source]¶

Transform triangle instance into a tabular representation.

Parameters: dropna (bool) – Should records with NA values be dropped? Default value is True.
Returns
Return type: pd.DataFrame

property triind¶

Table indicating forecast cells with 1, actual data with 0.

Returns
Return type: pd.DataFrame

class _BaseIncrTriangle(data, origin=None, dev=None, value=None)[source]¶: Internal incremental triangle class definition.

class IncrTriangle(data, origin=None, dev=None, value=None)[source]¶

Public incremental triangle class definition.

Parameters

data (pd.DataFrame) – The dataset to be transformed into a triangle instance. data must be tabular loss data with at minimum columns representing the origin/acident year, development period and value of interest, given by origin, dev and value respectively.
origin (str) – The fieldname in data representing origin year.
dev (str) – The fieldname in data representing development period.
value (str) – The fieldname in data representing loss amounts.

to_cum()[source]¶

Transform triangle instance into cumulative representation.

Returns
Return type: trikit.triangle.CumTriangle

class _BaseCumTriangle(data, origin='origin', dev='dev', value='value')[source]¶

Internal cumulative triangle class definition. Transforms data into a cumulative triangle instance.

Parameters

data (pd.DataFrame) – The dataset to be transformed into a triangle instance. data must be tabular loss data with at minimum columns representing the origin/acident year, development period and incremental value of interest, given by origin, dev and value respectively.
origin (str) – The fieldname in data representing the origin year.
dev (str) – The fieldname in data representing the development period.
value (str) – The fieldname in data representing incremental loss amounts.

static _geometric(vals, weights=None)[source]¶

Compute the geometric average of the elements of vals.

Parameters

vals (np.ndarray) – An array of values, typically representing link ratios from a single development period.
weights (np.ndarray) – Not yet implemented.

Returns

Return type

float

static _medial(vals, weights=None)[source]¶

Compute the medial average of elements in vals. Medial average eliminates the min and max values, then returns the arithmetic average of the remaining items.

Parameters

vals (np.ndarray) – An array of values, typically representing link ratios from a single development period.
weights (np.ndarray) – Weights to assign specific values in the average computation. If None, each value is assigned equal weight.

Returns

Return type

float

static _simple(vals, weights=None)[source]¶

Compute the simple average of elements of vals.

Parameters

vals (np.ndarray) – An array of values, typically representing link ratios from a single development period.
weights (np.ndarray) – Not yet implemented.

Returns

Return type

float

property a2a¶

Compute adjacent proportions, a.k.a. link ratios.

Returns
Return type: pd.DataFrame

property a2a_assignment¶

Identify triangle age-to-age factors into high and low categories based on value relative to the median for a given development period. Factors in excess of the median are assigned a value of +1. Age-to-age factors with value less than the median are assigned a value of -1. For development periods with an odd number of values, the true median is set to 0. Returned DataFrame has same dimensionality as self.tri.a2a.

Returns
Return type: pd.DataFrame

a2a_avgs()[source]¶

Compute age-to-age factors based on self.a2a table of adjacent proportions. Averages computed include “simple”, “geometric”, “medial” and “weighted”.

Returns
Return type: pd.DataFrame

property a2a_lvi¶

Reference to last valid index for triangle age-to-age factors.

Returns
Return type: pd.DataFrame

property a2aind¶

Determine which cells should be included and which to exclude when computing age-to-age averages. Cells populated with 1 are included, cells populated with 0 are excluded.

Returns
Return type: pd.DataFrame

property ranked_a2a¶

Construct triangle of ranked age-to-age factors for use in development period correlation testing.

Returns
Return type: pd.DataFrame

class CumTriangle(data, origin=None, dev=None, value=None)[source]¶

Cumulative triangle class definition.

_combined_view(**kwargs)[source]¶

Visualize triangle loss development using a combined view.

Parameters

cmap (str) – Selected matplotlib color map. For additional options, visit: https://matplotlib.org/tutorials/colors/colormaps.html.
kwargs (dict) – Additional plot styling options.

_faceted_view(color='#334488', axes_style='darkgrid', context='notebook', col_wrap=4, **kwargs)[source]¶

Visualize triangle loss development using a faceted view.

Parameters

color (str) – Color to plot loss development in each facet. Default value is “#334488”.
axes_style (str) – Aesthetic style of plots. Defaults to “darkgrid”. Other options include: {whitegrid, dark, white, ticks}.
context (str) – Set the plotting context parameters. According to the seaborn documentation, This affects things like the size of the labels, lines, and other elements of the plot, but not the overall style. Defaults to "notebook". Additional options include {“paper”, “talk”, “poster”}.
kwargs (dict) – Additional plot styling options.

base_cl(sel='all-weighted', tail=1.0)[source]¶

Produce chain ladder reserve estimates based on cumulative triangle instance.

Parameters

sel (str, pd.Series or array_like) – If sel is a string, the specified loss development patterns will be the associated entry from self.tri.a2a_avgs. If sel is array_like, values will be used in place of loss development factors computed from the traingle directly. For a triangle with n development periods, sel should be array_like with length n - 1. Defaults to “all-weighted”.
tail (float) – Chain ladder tail factor. Defaults to 1.0.

Examples

Generate chain ladder reserve point estimates using the raa dataset. tri is first created using the raa dataset:

In [1]: import trikit
In [2]: tri = trikit.load("raa", tri_type="cum")
In [4]: cl = tri.base_cl()

Perform standard chain ladder, using non-default values for sel and tail:

In [5]: cl = tri.base_cl(sel="medial-5", tail=1.015)

Passing a custom sequence of loss development factors:

In [6]: ldfs = [5., 2.5, 1.25, 1.15, 1.10, 1.05, 1.025, 1.01, 1.005,]
In [7]: cl = tri.base_cl(sel=ldfs, tail=1.001)

boot_cl(sims=1000, q=[0.75, 0.95], procdist='gamma', parametric=False, two_sided=False, interpolation='linear', random_state=None)[source]¶

Estimate reserves and the distribution of reserve outcomes by origin and in total via bootstrap resampling. The estimated distribution of losses assumes development is completen by the final development period in order to avoid the complication of modeling a tail factor.

Parameters

sims (int) – The number of bootstrap simulations to perform. Defaults to 1000.
q (array_like of float or float) – Quantile or sequence of quantiles to compute, which must be between 0 and 1 inclusive.
procdist (str) – The distribution used to incorporate process variance. Currently, this can only be set to “gamma”.
two_sided (bool) – Whether to include the two_sided interval in summary output. For example, if two_sided==True and q=.95, the 2.5th and 97.5th quantiles of the bootstrapped reserve distribution will be returned [(1 - .95) / 2, (1 + .95) / 2]. When False, only the specified quantile(s) will be computed. Defaults to False.
parametric (bool) – If True, fit standardized residuals to a normal distribution via maximum likelihood, and sample from the resulting distribution. Otherwise, values are sampled with replacement from the collection of standardized residuals. Defaults to False.
interpolation ({"linear", "lower", "higher", "midpoint", "nearest"}) – Optional parameter which specifies the interpolation method to use when the desired quantile lies between two data points i < j. See numpy.quantile for more information. Default value is “linear”.
random_state (np.random.RandomState) – If int, random_state is the seed used by the random number generator; If RandomState instance, random_state is the random number generator; If None, the random number generator is the RandomState instance used by np.random.

Returns

Return type

BootstrapChainLadderResult

Examples

Generate boostrap chain ladder reserve estimates. tri is first created using the raa dataset:

In [1]: import trikit
In [2]: tri = trikit.load("raa", tri_type="cum")
In [3]: bcl = tri.boot_cl()

glm(var_power=1)[source]¶: Generate reserve estimates via Generalized Linear Model framework. Note that glm_estimator assumes development is complete by the final development period. GLMs are fit using statsmodels Tweedie family with log link.

mack_cl(alpha=1, tail=1.0, dist='lognorm', q=[0.75, 0.95], two_sided=False)[source]¶

Return a summary of ultimate and reserve estimates resulting from the application of the development technique over self.tri. Summary DataFrame is comprised of origin year, maturity of origin year, loss amount at latest evaluation, cumulative loss development factors, projected ultimates and the reserve estimate, by origin year and in aggregate.

### TODO ### Allow for tail factor other than 1.0.

Parameters

alpha ({0, 1, 2}) –
- 0: Straight average of observed individual link ratios.
- 1: Historical Chain Ladder age-to-age factors.
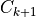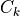- 2: Regression of $C_{k+1}$ on $C_{k}$ with 0 intercept.
tail (float) – Tail factor. Currently not implemented. Will be available in a future release.
dist ({"norm", "lognorm"}) –
The distribution function chosen to approximate the true distribution of reserves by origin period. In Mack[1], if the volume of outstanding claims is large enough, due to the central limit theorem, we can assume that the distribution function is Normal with expected value equal to the point estimate given by 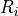$R_{i}$ and standard deviation equal to the standard error of 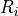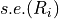$R_{i}$ , $s.e.(R_{i})$ . It is also noted that if the true distribution of reserves is skewed, the Normal may not serve as a good approximation, and it may be preferrable to opt for the Log-normal distribution.
- If dist="norm", the Normal distribution will be used to
estimate reserve quantiles.
- If dist="lognorm", the Log-normal distribution will be used
to estimate reserve quantiles.
q (array_like of float) – Quantile or sequence of quantiles to compute, which must be between 0 and 1 inclusive.
two_sided (bool) – Whether the two_sided interval should be included in summary output. For example, if two_sided==True and q=.95, then the 2.5th and 97.5th quantiles of the estimated reserve distribution will be returned [(1 - .95) / 2, (1 + .95) / 2]. When False, only the specified quantile(s) will be computed. Defaults to False.

Returns

Return type

MackChainLadderResult

Examples

Generate Mack chain ladder reserve estimates. tri is first created using the raa dataset. In the call to mack_cl, alpha is set to 2, and two_sided=True:

In [1]: import trikit
In [2]: tri = trikit.load("raa", tri_type="cum")
In [3]: mcl = tri.mack_cl(alpha=2, two_sided=True)

plot(display='combined', **kwargs)[source]¶

Plot cumulative loss development over a single set of axes or as faceted-by-origin exhibit.

Parameters

view ({"combined", "faceted"}) – Whether to display cumulative loss development in a single or faceted view. Default value is "combined".
kwargs (dict) –
Options for combined view:

cmap: str
Selected matplotlib color map. For additional options, visit: https://matplotlib.org/tutorials/colors/colormaps.html.

Options for faceted view:

color: str
Color to plot loss development in each facet. Default value is “#334488”.

axes_style: str
Aesthetic style of plots. Defaults to “darkgrid”. Other options include: {whitegrid, dark, white, ticks}.

context: str
Set the plotting context parameters. According to the seaborn documentation, This affects things like the size of the labels, lines, and other elements of the plot, but not the overall style. Defaults to "notebook". Additional options include {“paper”, “talk”, “poster”}.

to_incr()[source]¶

Obtain incremental triangle based on cumulative triangle instance.

Returns
Return type: trikit.triangle.IncrTriangle

Examples

Convert existing cumulative triangle instance into an instance of trikit.triangle.IncrTriangle:

In [1]: from trikit import load, totri
In [2]: cumtri = totri(load("raa"))
In [3]: incrtri = cumtri.to_incr()
In [4]: type(incrtri)
Out[4]: triangle.IncrTriangle